Sistem pertidaksamaan linear dua variabel berupa beberapa pertidaksamaan linear yang terdiri dari 2 variabel, biasanya
x atau
y (walaupun jenis variabel lainnya tetap memungkinkan). Pertidaksamaan linear dua variabel memiliki bentuk umum seperti berikut:
ax + by < c, ax + by > c, ax + by ≤ c, atau ax + by ≥ c
Sebelum menggambar daerah penyelesaian sistem pertidaksamaan linear
dua variabel, sebaiknya kita tahu terlebih dahulu mengenai himpunan
penyelesaian.
Himpunan penyelesaian merupakan himpunan pengganti nilai variabel sedemikian sehingga menyebabkan sistem pertidaksamaan menjadi
pernyataan yang benar.
Daerah penyelesaian yang akan kita gambar merupakan daerah dari
himpunan penyelesaian tersebut. Daerah ini berisi himpunan pasangan
berurutan (
x,
y) yang menjadi anggota dari himpunan penyelesaian.
Untuk menggambar daerah penyelesaian sistem pertidaksamaan linear dua variabel, perhatikan contoh soal berikut.
Contoh Soal
Gambarlah daerah penyelesaian dari sistem pertidaksamaan linear berikut untuk
x,
y anggota bilangan real.
–x + 8y ≤ 80
2x – 4y ≤ 5
2x + y ≥ 12
2x – y ≥ 4
x ≥ 0, y ≥ 0
Pembahasan Contoh Soal
Untuk menggambar daerah penyelesaian dari sitem pertidaksamaan yang dimaksud, lakukan langkah-langkah berikut:
Langkah pertama. Ubahlah
pertidaksamaan-pertidaksamaan yang dimaksud menjadi persamaan linear,
kemudian gambarkan persamaan linear tersebut pada bidang koordinat.
Grafik dari persamaan linear berupa garis lurus. Untuk itu, cari dua
titik yang dilewati oleh garis tersebut, kemudian hubungkan kedua titik
tersebut menjadi suatu garis lurus. Dua titik ini biasanya dipilih titik
pada sumbu-
x dan sumbu-
y, akan tetapi apabila kurang memungkinkan, pilihlah titik-titik lain.
Sehingga garis –
x + 8
y = 80 melalui titik-titik (0,
10) dan (16, 12). Dengan cara yang sama, dapat dicari 2 titik yang
dilalui persamaan garis lainnya.
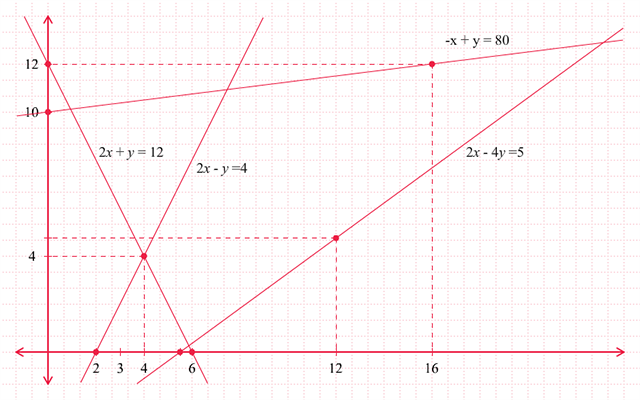
Sehingga, garis-garis dari –
x + 4
y = 80, 2
x – 4
y = 5, 2
x +
y = 12, dan 2
x –
y = 4 dapat digambarkan seperti berikut.
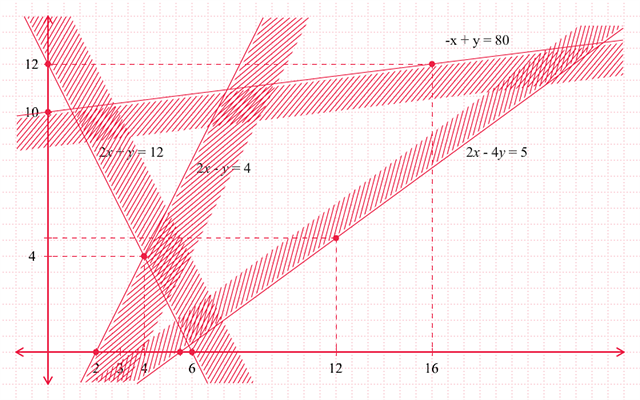
Langkah kedua. Arsirlah daerah dari masing-masing
pertidaksamaan. Untuk menentukan daerah pertidaksamaan, pilihlah salah
satu titik yang terdapat di kanan atau di kiri, atas atau bawah dari
garis. Apabila koordinat titik tersebut disubstitusikan ke dalam
pertidaksamaan dan menghasilkan pernyataan yang benar, maka daerah titik
tersebut merupakan daerah penyelesaian pertidaksamaan tersebut.
Arsirlah daerah penyelesaian tersebut. Sebaliknya, apabila koordinat
titik tersebut disubstitusikan ke dalam pertidaksamaan dan menghasilkan
pernyataan yang salah, maka daerah titik tersebut bukan merupakan daerah
penyelesaian pertidaksamaan tersebut. Arsirlah daerah yang
berseberangan terhadap titik tersebut. Misalkan kita akan menemukan
daerah penyelesaian dari pertidaksamaan –
x + 8
y ≤ 80.
Misalkan kita pilih titik (0, 12) yang terletak di atas garis sebagai
titik uji. Kita substitusikan ke dalam pertidaksamaan sebagai berikut.
Dengan mensubstitusikan titik (0, 12) ke pertidaksamaan –
x + 8
y
≤ 80 menghasilkan pernyataan yang salah, sehingga daerah yang memuat
titik (0, 12) bukan penyelesaian dari pertidaksamaan tersebut. Sehingga
daerah yang berlawanan dengan daerah tersebut, yaitu daerah bawah, yang
kita arsir.
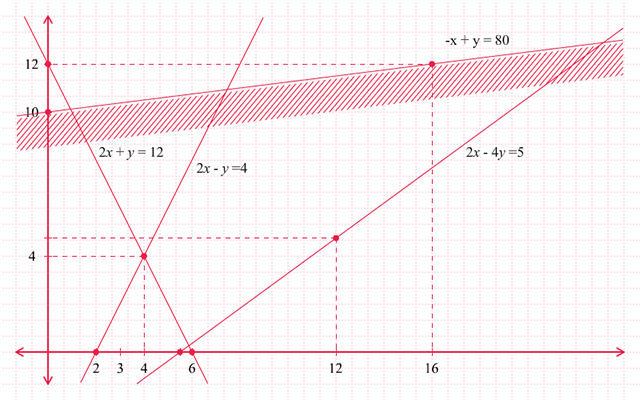
Dengan cara yang sama, kita cari daerah penyelesaian dari
pertidaksamaan-pertidaksamaan lainnya. Setelah itu kita gambarkan
daerahnya seperti pada gambar berikut.
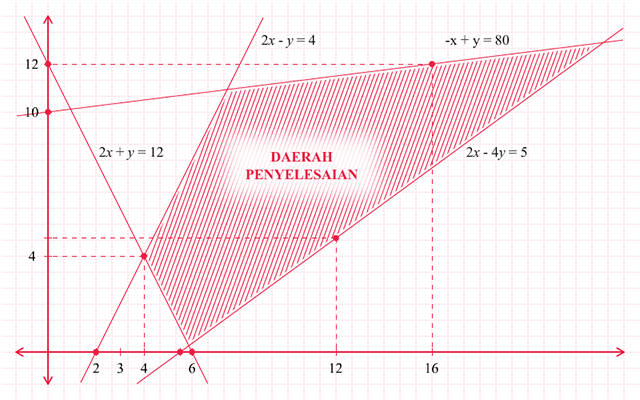
Langkah ketiga. Arsirlah daerah himpunan
penyelesaian dari sistem pertidaksamaan yang dimaksud. Himpunan
penyelesaian dari sistem pertidaksamaan merupakan irisan dari himpunan
penyelesaian dari masing-masing pertidaksamaan. Atau secara visual,
daerah penyelesaian dari sistem pertidaksamaan merupakan daerah yang
terkena arsiran dari semua daerah penyelesaian. Sehingga himpunan
penyelesaian dari pertidaksamaan –
x + 8
y ≤ 80, 2
x – 4
y ≤ 5, 2
x +
y ≥ 12, 2
x –
y ≥ 4,
x ≥ 0, dan
y ≥ 0 dapat digambarkan sebagai berikut.
sumber: http://yos3prens.wordpress.com
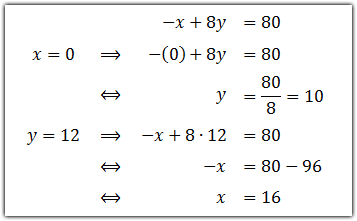

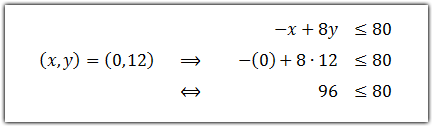
No comments:
Post a Comment